How Many Three-digit Numbers Less Than 600 Can Be Made Using the Digits 8, 6, 4, and 2?

Binary Calculator

Use the following calculators to perform the add-on, subtraction, multiplication, or segmentation of ii binary values, as well equally catechumen binary values to decimal values, and vice versa.

Binary Calculation—Add together, Subtract, Multiply, or Separate

= ?

Convert Binary Value to Decimal Value

Binary Value: = ?

Convert Decimal Value to Binary Value

Decimal Value: = ?

The binary organization is a numerical system that functions well-nigh identically to the decimal number system that people are probable more familiar with. While the decimal number system uses the number x equally its base, the binary organisation uses 2. Furthermore, although the decimal system uses the digits 0 through nine, the binary organisation uses only 0 and 1, and each digit is referred to as a bit. Apart from these differences, operations such as addition, subtraction, multiplication, and sectionalization are all computed post-obit the aforementioned rules every bit the decimal system.

Nearly all mod engineering and computers use the binary system due to its ease of implementation in digital circuitry using logic gates. It is much simpler to design hardware that only needs to find two states, on and off (or truthful/simulated, present/absent, etc.). Using a decimal system would crave hardware that can detect 10 states for the digits 0 through 9, and is more than complicated.

Below are some typical conversions betwixt binary and decimal values:

Binary/Decimal Conversion

Decimal	Binary
0	0
1	1
2	x
3	11
4	100
7	111
8	1000
10	1010
16	10000
20	10100

While working with binary may initially seem disruptive, understanding that each binary place value represents 2^{due north}, just as each decimal place represents xⁿ, should help analyze. Take the number eight for case. In the decimal number system, 8 is positioned in the outset decimal place left of the decimal point, signifying the x⁰ identify. Essentially this ways:

eight × 10⁰ = 8 × 1 = 8

Using the number eighteen for comparing:

(1 × 10¹) + (8 × 10⁰) = ten + 8 = 18

In binary, 8 is represented as 1000. Reading from right to left, the first 0 represents 2⁰, the second 2¹, the 3rd 2², and the fourth ii³; just like the decimal organization, except with a base of 2 rather than 10. Since 2³ = eight, a 1 is entered in its position yielding g. Using xviii, or 10010 equally an example:

18 = 16 + 2 = two^iv + 2^one
10010 = (1 × two^iv) + (0 × 2³) + (0 × iiⁱⁱ) + (1 × 2ⁱ) + (0 × 2⁰) = eighteen

The stride by step process to convert from the decimal to the binary organization is:

1. Find the largest power of 2 that lies within the given number
2. Subtract that value from the given number
3. Find the largest power of 2 within the remainder constitute in stride two
4. Repeat until there is no remainder
5. Enter a 1 for each binary place value that was found, and a 0 for the residuum

Using the target of 18 again as an case, beneath is another way to visualize this:

iinorthward	24	two3	2ii	two1	two0
Instances within 18	ane	0	0	1	0
Target: 18	18 - 16 = 2	→		two - 2 = 0

Converting from the binary to the decimal system is simpler. Determine all of the place values where 1 occurs, and find the sum of the values.

EX: 10111 = (1 × two⁴) + (0 × two³) + (1 × 2²) + (1 × 2¹) + (1 × 2⁰) = 23

24	twothree	22	2ane	20
1	0	i	one	1
16	0	4	ii	1

Hence: 16 + 4 + 2 + i = 23.

Binary Addition

Binary improver follows the aforementioned rules as addition in the decimal organisation except that rather than conveying a ane over when the values added equal 10, carry over occurs when the result of addition equals 2. Refer to the example beneath for clarification.

Note that in the binary system:

0 + 0 = 0
0 + one = i
ane + 0 = 1
1 + ane = 0, carry over the 1, i.east. 10

EX:

		10	1i	11	i0	1
+		1	0	ane	1	ane
=	1	0	0	1	0	0

The only real difference between binary and decimal addition is that the value 2 in the binary system is the equivalent of 10 in the decimal system. Note that the superscripted 1'due south represent digits that are carried over. A common mistake to watch out for when conducting binary add-on is in the case where ane + 1 = 0 also has a 1 carried over from the previous cavalcade to its correct. The value at the bottom should and then exist 1 from the carried over 1 rather than 0. This can be observed in the 3rd column from the right in the to a higher place case.

Binary Subtraction

Similar to binary addition, there is little difference between binary and decimal subtraction except those that arise from using simply the digits 0 and 1. Borrowing occurs in whatever example where the number that is subtracted is larger than the number it is being subtracted from. In binary subtraction, the only example where borrowing is necessary is when 1 is subtracted from 0. When this occurs, the 0 in the borrowing column essentially becomes "2" (irresolute the 0-i into ii-ane = one) while reducing the i in the column being borrowed from by 1. If the post-obit column is also 0, borrowing will accept to occur from each subsequent column until a cavalcade with a value of ane can exist reduced to 0. Refer to the example below for clarification.

Note that in the binary system:

0 - 0 = 0
0 - 1 = 1, borrow ane, resulting in -ane carried over
i - 0 = 1
one - ane = 0

EX1:

		-1ane	20	one	1	1
–		0	1	1	0	i
=		0	1	0	1	0

EX2:

		-1i	2-ane0	0
–		0	one	1
=		0	0	one

Notation that the superscripts displayed are the changes that occur to each bit when borrowing. The borrowing column essentially obtains 2 from borrowing, and the column that is borrowed from is reduced by ane.

Binary Multiplication

Binary multiplication is arguably simpler than its decimal counterpart. Since the only values used are 0 and 1, the results that must be added are either the aforementioned as the first term, or 0. Notation that in each subsequent row, placeholder 0's need to exist added, and the value shifted to the left, just like in decimal multiplication. The complexity in binary multiplication arises from ho-hum binary addition dependent on how many bits are in each term. Refer to the case below for clarification.

Note that in the binary arrangement:

0 × 0 = 0
0 × i = 0
1 × 0 = 0
one × one = i

EX:

			1	0	one	1	ane
×						ane	1
			1	0	ane	ane	1
+		1	0	i	1	1	0
=	i	0	0	0	one	0	1

As can be seen in the example to a higher place, the process of binary multiplication is the same every bit it is in decimal multiplication. Note that the 0 placeholder is written in the second line. Typically the 0 placeholder is not visually present in decimal multiplication. While the same can exist washed in this example (with the 0 placeholder beingness causeless rather than explicit), it is included in this example considering the 0 is relevant for any binary addition / subtraction calculator, like the 1 provided on this page. Without the 0 existence shown, it would be possible to make the mistake of excluding the 0 when adding the binary values displayed in a higher place. Note once more that in the binary arrangement, whatsoever 0 to the right of a 1 is relevant, while any 0 to the left of the last 1 in the value is non.

EX:

1 0 1 0 ane 1 0 0
= 0 0 one 0 1 0 one 1 0 0
≠ 1 0 ane 0 1 1 0 0 0 0

Binary Segmentation

The procedure of binary partition is like to long division in the decimal system. The dividend is yet divided by the divisor in the same manner, with the only significant difference existence the use of binary rather than decimal subtraction. Annotation that a good agreement of binary subtraction is of import for conducting binary division. Refer to the instance below, as well as to the binary subtraction section for clarification.

serpamannever.blogspot.com

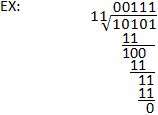
Source: https://www.calculator.net/binary-calculator.html

Share this post